|
固定频率升压转换器非常适合于以恒流模式驱动LED串。这种转换器采用不连续导电模式(DCM)工作,能够有效地用于快速调光操作,提供比采用连续导电模式(CCM)工作的竞争器件更优异的瞬态响应。当LED导通时,DCM工作能够提供快速的瞬态性能,为输出电容重新充电,因而将LED的模拟调光降至最低。为了恰当地稳定DCM升压转换器,存在着小信号模型。然而,驱动LED的升压转换器的交流分析,跟使用标准电阻型负载的升压转换器的交流分析不同。由于串联二极管要求直流和交流负载条件,在推导最终的传递函数时必须非常审慎。
本文(即第1部分)不会使用不连续导电模式(DCM)升压转换器的传统小信号模型,而将使用基于所研究转换器之输出电流表达式的简化方法。在第2部分(实际考虑),我们将深入研究应用方案,验证测量精度,并与理论推导进行比较。
为LED串供电的升压转换器图1显示了驱动LED串的恒定频率峰值电流工作模式升压转换器的简化电路图。输出电流被感测电阻Rsense持续监测。相应的输出电压施加在控制电路上,持续调节电源开关的导通时间,以提供恒定的LED电流Iout.这就是受控的输出变量。
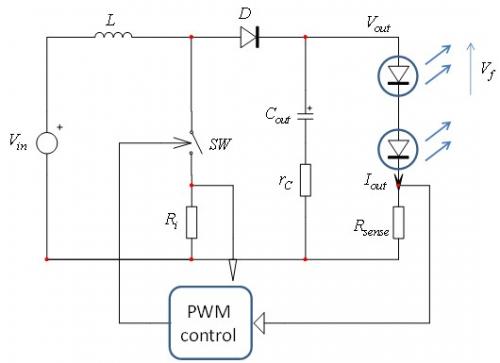
图1驱动LED串以发光的升压转换器。输出电流被稳流至设定点值。
发光时,LED串会在LED连接的两端产生电压。这电压取决于跟各个LED技术相关的阈值电压VT0及其动态阻抗rd.因此,LED串两端的总压降就是各LED阈值电压之和VZ,而而动态阻抗rLEDs表示的是LED串联动态阻抗之和。图2显示的是采用的等效电路。您可以自己来对LED串压降及其总动态阻抗进行特征描述。为了测量起见,将LED串电流偏置至其额定电流IF1.一旦LED达到热稳定,就测量LED串两端的总压降Vf1.将电流改变为稍低值IF2并测量新的压降VF2.根据这些值,您可计算出总动态阻抗,即:
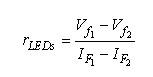 (1) (1)
"齐纳"电压约等于LED串电压VF1减去rLEDs与测量点电流之积:
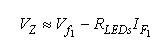 (2) (2)
我们假定以100 mA电流来偏置我们的LED串。测量出的总压降为27.5 V.我们将电流减小至80 mA,新得到的压降值就是26.4 V.总动态阻抗的计算很简单:
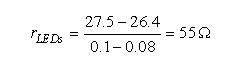 (3) (3)
根据等式(2),我们可以简单地计算出齐纳电压:
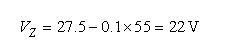 (4) (4)
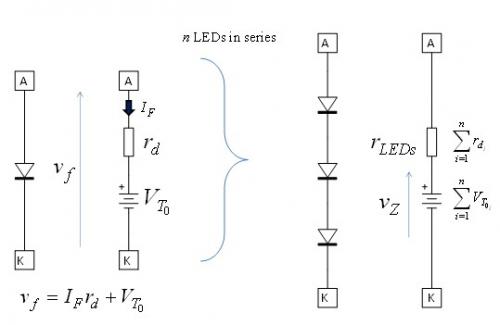
图2:LED采用串联连接,故需对它们的阈值电压进行累加;而总动态阻抗是串联连接的各个LED动态阻抗之和。
回头再看图1.LED串与感测电阻Rsense串联。总交流(ac)阻抗因此就是两者之和:
 (5) (5)
图3是大幅简化的等效直流(dc)电路图。直流输出电压Vout等于输出电流Iout与电阻Rac之积再加齐纳电压:
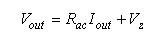 (6) (6)
在交流条件下,由于齐纳电压恒定,故上述等式可简化为:
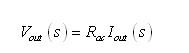 (7) (7)
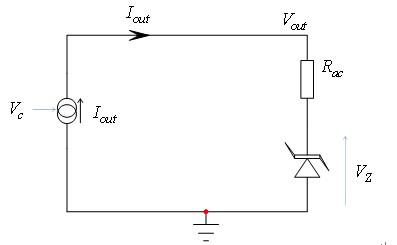
图3:这直流简化电路图显示了等效齐纳二极管及其动态阻抗。
简化模型电流源实际上指的是从输入电源获得并无损耗地传输到输出的电流。电流源可以被控制电压Vc向上或向下调节,而Vc逐周期设定电感峰值电流。控制器通过升压转换器开关电流感测电阻Ri来观测电感峰值电流,并以此工作。当Ri两端电压与控制电压匹配时,电源开关就被指示关闭。
如果我们现在来考虑交流电路图,就要考虑电容及其寄生元件,如图4所示。齐纳元件自身并无影响,因为在交流调制期间其电压保持恒定:仅其动态阻抗rLEDs需要予以考虑,融合到Rac中。如等式(5)所述。
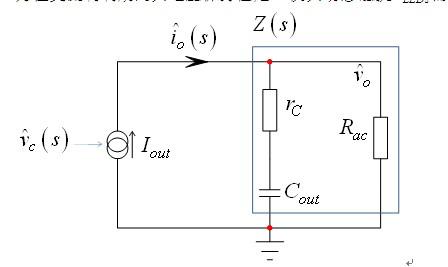
图4:交流模型使用跟电容模型相关的总阻抗Rac.
根据此图,有可能表达出控制电压被调制时的小信号输出电压电平:
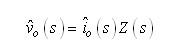 (8) (8)
如前所述,电流源值取决于控制及输出电压。为了推导出小信号等效模型,我们解析了跟控制电压Vc及输出电压Vout相关的Iout偏导数:
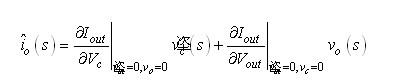 (9) (9)
结合等式(9),可以改写等式(8)如下:
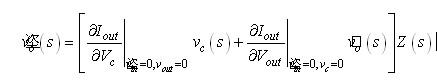 (10) (10)
参考资料[1] (等式1-111,第49页)已经推导出DCM升压转换器直流传递函数,即:
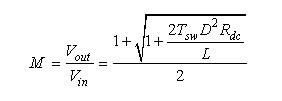 (11) (11)
在此等式中,转换器的直流阻抗(Rdc)必须以替代。新的等式就变成:
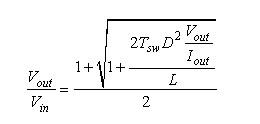 (12) (12)
我们需要根据这个等式推导出占空比(D)的等式及控制电压Vc.在存在补偿斜坡的情况下,控制电压不再是固定的直流电压,而是斜率会影响最终峰值电流设定点的斜坡电压。图5显示了最终波形。到达峰值电流值的时间比不存在斜坡的情况下更快,就好像我们会人为增加电流控制感测电阻Ri一样。它有降低电流控制环路增益及降低连续导电模式(CCM)下两个极点的作用。当转换器过渡到DCM时,仍然存在斜坡,必须予以顾及。
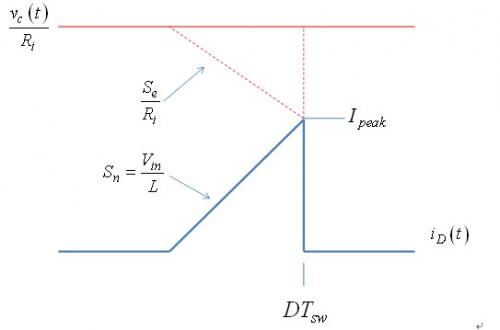
图5:由于补偿斜坡的缘故,峰值电流并不等于控制电压除以Rsense.相关等式如下所示,其中考虑到了比例因数Ri,因为外部斜波Se是电压斜波:
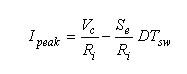 (13) (13)
可以推导出涉及至电感电流斜率的类似等式:
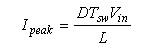 (14) (14)
解析占空比D,我们就得到:
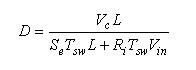 (15) (15)
将这个等式代入等式(12)中,我们就解算出输出电流Iout:
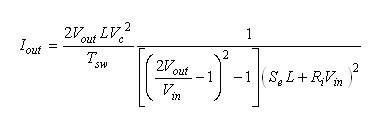 (16) (16)
为了获得小信号值,我们就像等式(10)一样,计算Iout跟控制电压Vc和输出电压Vout相关的偏导数:(17)
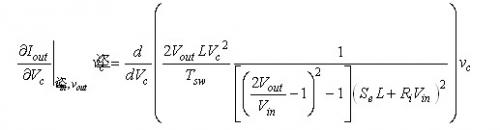 (18) (18)
这个等式描述了vc的小信号模型对输出电流的影响。
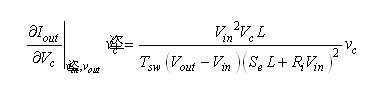 (19) (19)
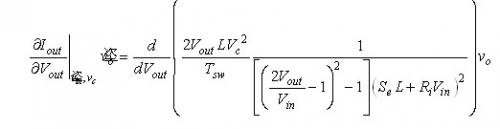 (20) (20)
等式(20)表述了电流跟电压与一个大小为电导g的系数之乘积的相关关系。
它是一个压控电流源,如图6所示。
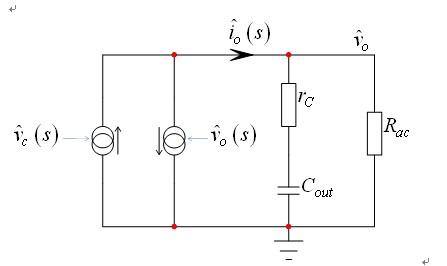
图6:等式(20)中的系数是压控电流源,为阻抗。
由于等式(20)中的负号的缘故,电流方向被倒转。因此,由于我们有被电压驱动的电流源,它就相当于一个电阻,其定义如下:
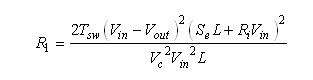 (21) (21)
在这个简化等式中,电流源指的是从输入源吸收并传输至输出的电能。电流源等式并不涵盖跟转换器工作模式相关的信息。例如,回头看等式(16),我们并不清楚器件工作在固定频率模式,在导通时间期间或是在关闭时间期间将电能传输至输出负载,诸如此类。在缺乏这类信息的情况下,明显要避开一些2阶成分,如右半平面零点(RHPZ)。然而,从前面的分析中我们知道,DCM工作中仍然存在RHPZ,但由于它被归为高频,在这种情况下我们可以忽视它的存在。这种简化方法的优势就是能够快速地推导出挖模型,为您提供所考虑架构的低频特性:直流增益和极点/零点组合。可以采用的另一种方法是使用DCM电流模式升压转换器的小信号模型,以由图4中元件组成的负载进行完整分析。这种方法将提供确切的结果,但会要求更多的迭代及复杂的等式。
完整交流模型既然我们已经推导出所有系数,我们就可以更新原先图4中中所示的模型。更新的电路图如图7所示。R1对应于等式(20)中的系数,并可推导出与输出电压调制直接成正比的电流。
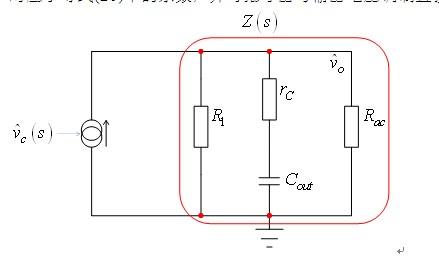
图7:我们将根据这更新的交流模型图计算出完整的传递函数。
为了推导所感兴趣的传递函数,我们将简化电路,审视电流源的负载阻抗Z.其定义如下:
 (22) (22)
在上述等式中,Req是Rac和R1的并联组合:
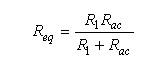 (23) (23)
因此,完整的传递函数就是等式(18)中给出的系数乘以等式(23)中的阻抗,也就是等式(22)给出的极点/零点组合阻抗Req:
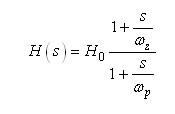 (24) (24)
其中,
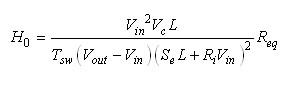 (25) (25)
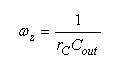 (26) (26)
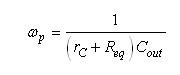 (27) (27)
推导工作点在推算交流函数之前,我们需要表达工作点及输出电流与控制电压Vc之间的相关性。我们知道输出电压等于:
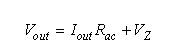 (28) (28)
我们可将这个定义代入等式(12)中:
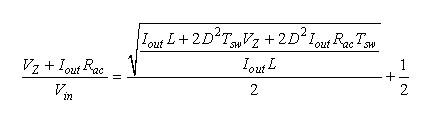 (29) (29)
根据这个等式,我们可以解析出Iout:
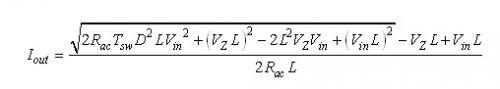 (30) (30)
我们也可以根据等式(15)替代占空比D.在这种情况下,输出电流等式就变得很繁杂,但也很有用:
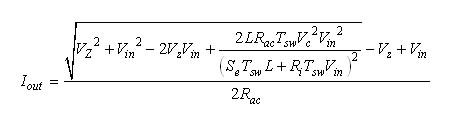 (31) (31)
根据这个等式,如果知道LED串电压VZ及其动态阻抗rLEDs,我们就可以预测升压转换器提供的电流。我们接下来以实际示例验证这些等式。
实际应用我们将使用下面的值来检验我们的计算。这是一款DCM升压转换器,为22 V压降的LED串提供恒定功率。
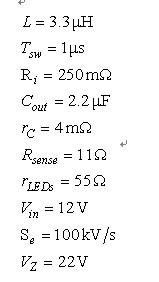
要计算出此电流,我们假定控制电压Vc为400 mV.我们能以等式(15)计算占空比:
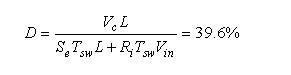 (32) (32)
从等式(31)可以获得输出电流:
 (33) (33)
然后又可以快速计算出输出电压:
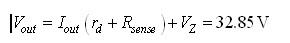 (34) (34)
等式(21)中计算的额外电阻R1的值计算如下:
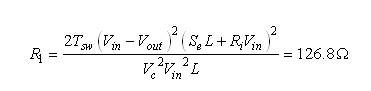 (35) (35)
当R1与Rac并联时,参照等式(23),就变成:
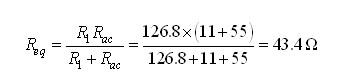 (36) (36)
我们现在可以计算静态增益H0:
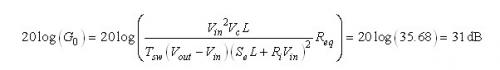 (37) (37)
推导出的极点和零点如下:
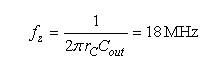 (38) (38)
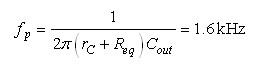 (39) (39)
可以运行SPICE仿真来检验此偏置点的有效性。我们使用了参考资料[1]中第161页推导出的大信号自动触发电流模型。电路图及反射的偏置点如图8所示。在此电路图中,为了获得正确的动态阻抗的工作电压,我们使用简单的分流稳压器模仿完美齐纳二极管的工作。这完美二极管提供22 V的击穿电压VZ,其动态阻抗为55。应当注意的是,简单的22 V直流源就能用于交流分析,但在诸如启动等任何瞬态仿真条件下就不适用。当运行交流扫描分时,SPICE将工作点周围的电路线性化,并产生小信号模型。电路图中显示的结果跟我们根据解析分析获得的结果相距不远。控制电压为0.4 V条件下感测电阻电流到达,接近于等式(33)中计算出的值。
受控系统波特图如图9所示。直接增益接近于等式(37)的计算结果,极点位于恰当位置(1.6 kHz)。相位持续下降是因为高频RHPZ位于高频率。我们的简化方法无法预测这RHPZ的存在。它存在与否跟拓扑结构的布设有关:升压转换器在导通时间期间先在电感中存储电源能量,并在关闭期间将其泄放给负载。任何负载变化,如输出电流增加,必须首先通过电感跃升,然后再提供给输出。这种工作模式固有的延迟通过RHPZ来建模。这能量传输延迟并不会明显地出现在等式(16)中,因为该等式简单地电流与控制电压Vc之间的关系。但在DCM条件下,等式(38)中定义的左半平面零点(LHPZ)在显著高于工作频率Fsw的频率时出现。
应当注意的是,我们在实际对LED电流进行稳流的时候分析了输出电压。在我们观测感测电阻Rsense两端的电压时,反馈信号是Vout按由rLEDs和Rsense构成的分压比例向下调节。比例调整就变为:
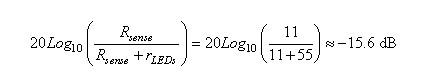 (40) (40)
这个曲线也表征在图8中。
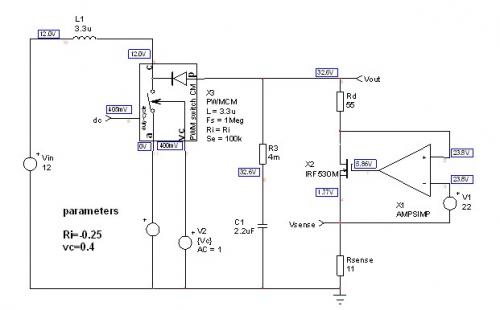
图8:平均模型帮助验证工作偏置点及交流响应。
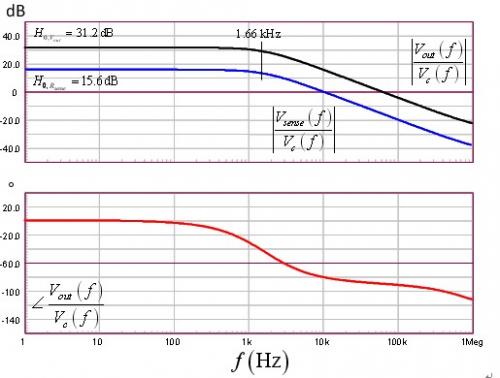
图9:波特图确认了直流增益及极点位置。
结论
这第1部分的文章介绍如何推导驱动LED串的升压转换器的小信号响应。本文没有应用DCM升压转换器的完整小信号模型,而是推导简单的等式,描述采用不连续导电模式工作的LED升压转换器的一阶响应。尽管存在一阶的固有局限,简要分析获得的答案是足以稳定控制环路。在第2部分(实际考虑因素)文章中,我们将深入研究实施方案,并验证经验结果及与理论推导比较。
|

